In One Corner…

As we saw in our Faster Group Statistics post, data.table is the heavyweight champ in the field. Its gforce functions and fast grouping put it head and shoulders above all challengers. And yet, here we are, about to throw our hat in the ring with nothing but base R functionality. Are we out of our minds?

Obviously I wouldn’t be writing this if I didn’t think we had a chance, although the only reason we have a chance is because data.table generously contributed its fast radix sort to R 3.3.0. Perhaps it is ungracious of us to use it to try to beat data.table, but where’s the fun in being gracious?

The Ring, and a Warmup

Ten million observations, ~one million groups, no holds barred:

RNGversion("3.5.2"); set.seed(42)
n     <- 1e7
n.grp <- 1e6
grp   <- sample(n.grp, n, replace=TRUE)
noise <- rep(c(.001, -.001), n/2)  # more on this later
x     <- runif(n) + noise
y     <- runif(n) + noise          # we'll use this later

Let’s do a warm-up run, with a simple statistic. We use vapply/split instead of tapply as that will allow us to work with more complex statistics later. sys.time is a wrapper around system.time that runs the expression eleven times and returns the median timing. It is defined in the appendix.

sys.time({
  grp.dat <- split(x, grp)
  x.ref <- vapply(grp.dat, sum, 0)
})

   user  system elapsed
  6.235   0.076   6.316

Let’s repeat by ordering the data first because pixie dust:

sys.time({
  o <- order(grp)
  go <- grp[o]
  xo <- x[o]

  grp.dat <- split(xo, go)
  xgo.sum <- vapply(grp.dat, sum, numeric(1))
})

   user  system elapsed 
  2.743   0.092   2.840 

And now with data.table:

library(data.table)
DT <- data.table(grp, x)
setDTthreads(1)             # turn off multi-threading
sys.time(x.dt <- DT[, sum(x), keyby=grp][[2]])

   user  system elapsed
  0.941   0.030   0.973

Ouch. Even without multithreading data.table crushes even the ordered split/vapply. We use one thread for more stable and comparable results. We’ll show some multi-threaded benchmarks at the end.

Interlude - Better Living Through Sorted Data

Pixie dust is awesome, but there is an even more important reason to like sorted data: it opens up possibilities for better algorithms. unique makes for a good illustration. Let’s start with a simple run:

sys.time(u0 <- unique(grp))

   user  system elapsed
  1.223   0.055   1.290

We are ~40% faster if we order first, including the time to order¹:

sys.time({
  o <- order(grp)
  go <- grp[o]
  u1 <- unique(go)
})

   user  system elapsed
  0.884   0.049   0.937

identical(sort(u0), u1)

[1] TRUE

The interesting thing is that once the data is ordered we don’t even need to use unique and its inefficient hash table. For example, in:

(go.hd <- head(go, 30))

 [1] 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4

We just need to find the positions where the values change to find the unique values, which we can do with diff, or the slightly-faster-for-this-purpose²:

go[-1L] != go[-length(go)]

It is clear looking at the vectors side by side that the groups change when they are not equal (showing first 30):

go[-1L]         : 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4
go[-length(go)] : 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4

To get the unique values we can just use the above to index into go, though we must offset by one element:

sys.time({
  o <- order(grp)
  go <- grp[o]
  u2 <- go[c(TRUE, go[-1L] != go[-length(go)])]
})

   user  system elapsed
  0.652   0.017   0.672

identical(u1, u2)

[1] TRUE

Same result, but twice the speed of the original, again including the time to order. Most of the time is spent ordering as we can see by how quickly we pick out the unique values once the data is ordered:

sys.time(u2 <- go[c(TRUE, go[-1L] != go[-length(go)])])

   user  system elapsed
  0.135   0.016   0.151

The main point I’m trying to make here is that it is a big deal that order is fast enough that we can switch the algorithms we use downstream and get an even bigger performance improvement.

A big thank you to team data.table for sharing the pixie dust.

Group Sums

It’s cute that we can use our newfound power to find unique values, but can we do something more sophisticated? It turns out we can. John Mount, shows how to compute group sums using cumsum on group-ordered data³. With a little work we can generalize it.

The concept is to order by group, compute cumulative sum, pull out the last value for each group, and take their differences. Visually:

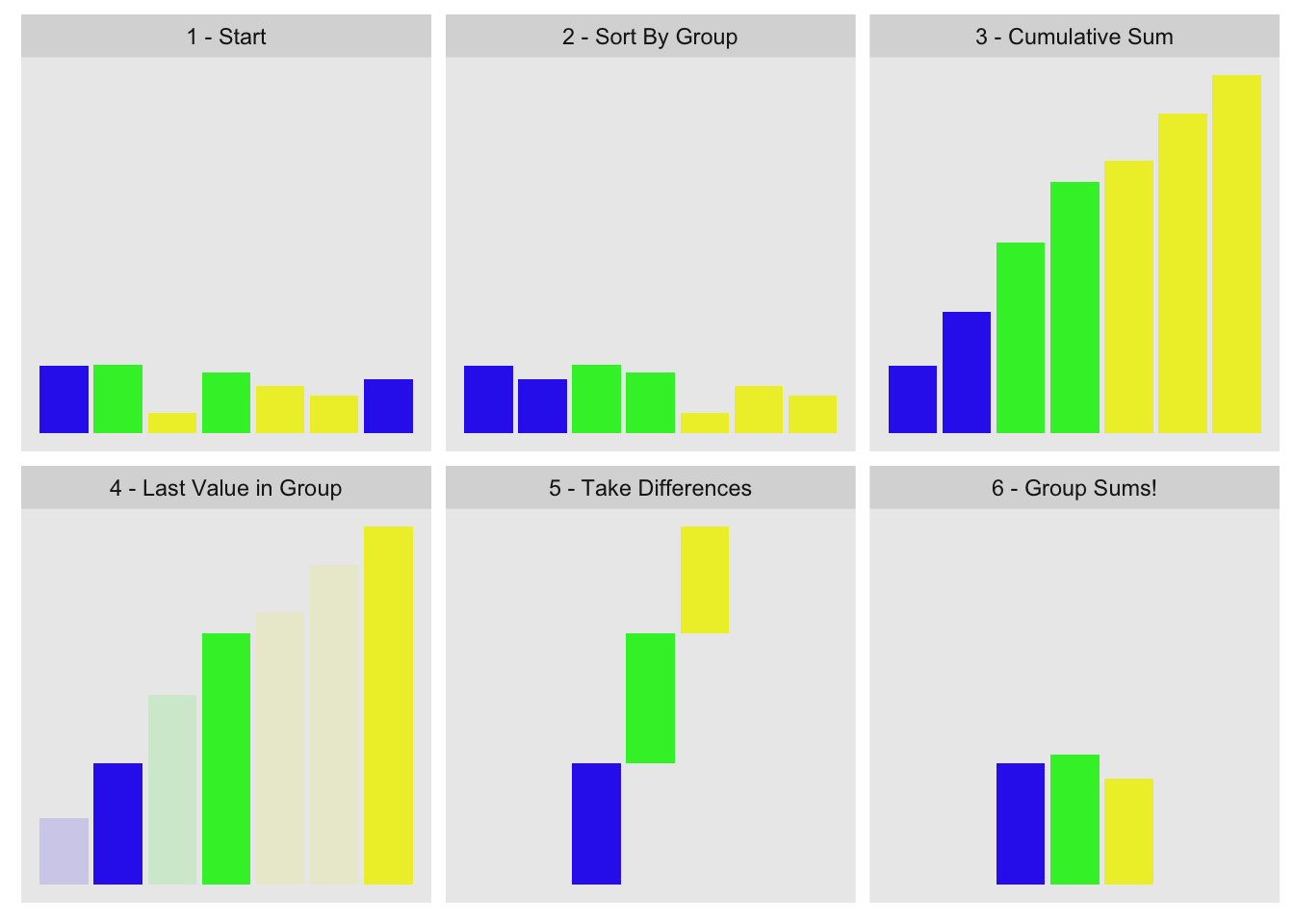
This is the data we used for the visualization:

g1

[1] 1 2 3 2 3 3 1

x1

[1] 0.915 0.937 0.286 0.830 0.642 0.519 0.737

The first three steps are obvious:

ord <- order(g1)
go <- g1[ord]
xo <- x1[ord]
xc <- cumsum(xo)

Picking the last value from each group is a little harder, but we can do so with the help of base::rle. rle returns the lengths of repeated-value sequences within a vector. In a vector of ordered group ids, we can use it to compute the lengths of each group:

go

[1] 1 1 2 2 3 3 3

grle <- rle(go)
(gn <- grle[['lengths']])

[1] 2 2 3

This tells us the first group has two elements, the second also two, and the last three. We can translate this into indices of the original vector with cumsum, and use it to pull out the relevant values from the cumulative sum of the x values:

(gnc <- cumsum(gn))

[1] 2 4 7

(xc.last <- xc[gnc])

[1] 1.65 3.42 4.87

To finish we just take the differences:

diff(c(0, xc.last))

[1] 1.65 1.77 1.45

I wrapped the whole thing into the group_sum function you can see in the appendix:

group_sum(x1, g1)

   1    2    3 
1.65 1.77 1.45 

Every step of group_sum is internally vectorized⁴, so the function is fast. We demonstrate here with the original 10MM data set:

sys.time(x.grpsum <- group_sum(x, grp))

   user  system elapsed
  1.098   0.244   1.344

all.equal(x.grpsum, c(x.ref), check.attributes=FALSE)

[1] TRUE

data.table is still faster, but we’re within striking distance. Besides, the real fight is up ahead.

Before we go on, I should note that R provides base::rowsum, not to be confused with its better known cousin base::rowSums. And why would you confuse them? Clearly the capitalization and pluralization provide stark semantic clues that distinguish them like dawn does night and day. Anyhow…, rowsum is the only base R function I know of that computes group statistics with arbitrary group sizes directly in compiled code. If all we’re trying to do is group sums, then we’re better off using that instead of our homegrown cumsum version:

sys.time({
  o <- order(grp)
  x.rs <- rowsum(x[o], grp[o], reorder=FALSE)
})

   user  system elapsed
  1.283   0.105   1.430

all.equal(x.grpsum, c(x.rs), check.attributes=FALSE)

[1] TRUE

A summary of timings so far:

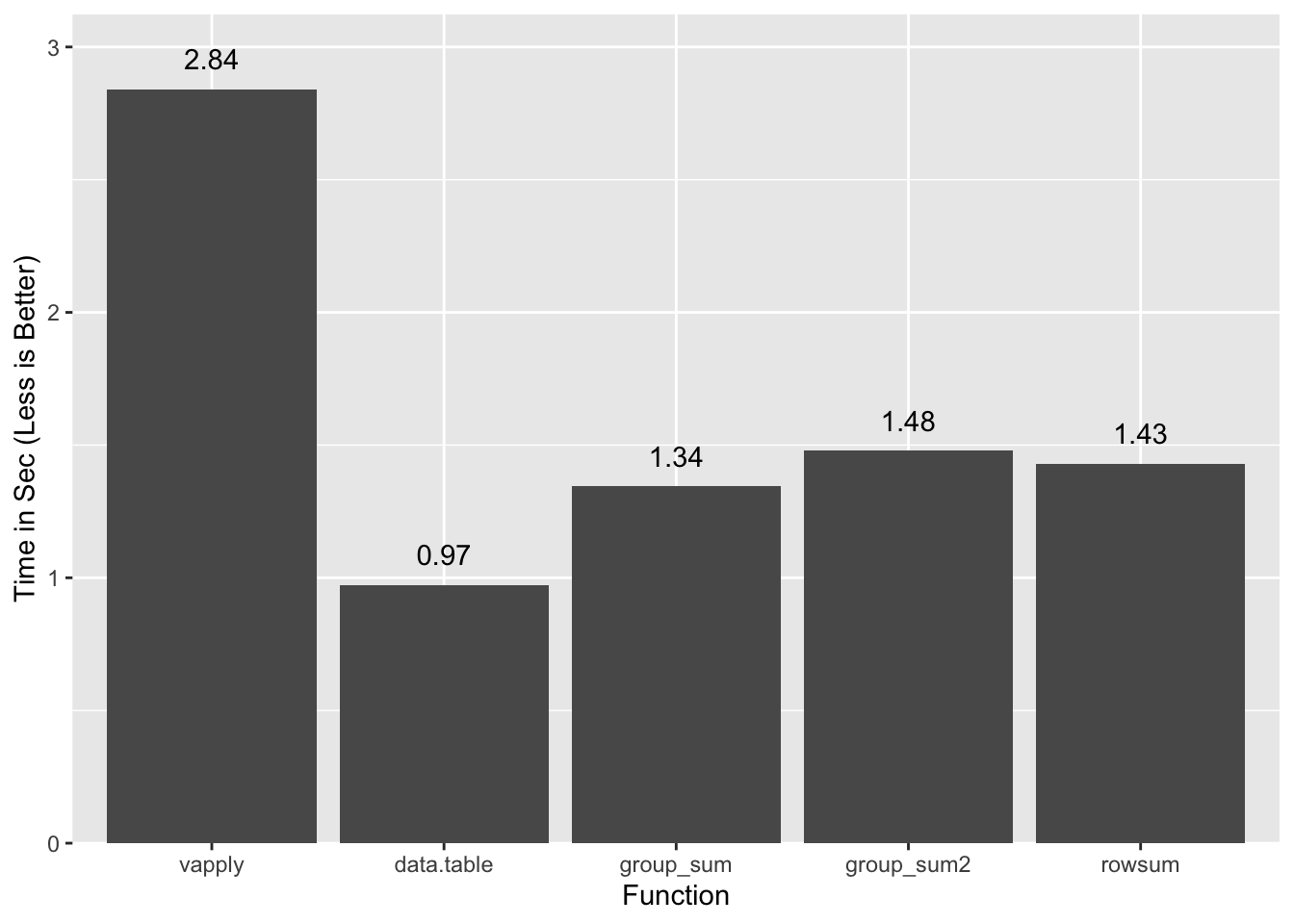
vapply/split and rowsum use ordered inputs and include the time to order them. data.table is single thread, and group_sum2 is a version of group_sum that handles NAs and infinite values. Since performance is comparable for group_sum2 we will ignore the NA/Inf wrinkle going forward.

So You Think You Can Group-Stat?

Okay, great, we can sum quickly in base R. One measly stat. What good is that if we want to compute something more complex like the slope of a bivariate regression, as we did in our prior post? As a refresher this is what the calculation looks like:

\[\frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sum(x_i - \bar{x})^{2}}\]

The R equivalent is⁵:

slope <- function(x, y) {
  x_ux <- x - mean.default(x)
  y_uy <- y - mean.default(y)
  sum(x_ux * y_uy) / sum(x_ux ^ 2)
}

We can see that sum shows up explicitly, and somewhat implicitly via mean⁶. There are many statistics that essentially boil down to adding things together, so we can use group_sum (or in this case its simpler form .group_sum_int) as the wedge to breach the barrier to fast grouped statistics in R:

.group_sum_int <- function(x, last.in.group) {
  xgc <- cumsum(x)[last.in.group]
  diff(c(0, xgc))
}
group_slope <- function(x, y, grp) {
  ## order inputs by group
  o <- order(grp)
  go <- grp[o]
  xo <- x[o]
  yo <- y[o]

  ## group sizes and group indices
  grle <- rle(go)
  gn <- grle[['lengths']]
  gnc <- cumsum(gn)              # Last index in each group
  gi <- rep(seq_along(gn), gn)   # Group recycle indices

  ## compute mean(x) and mean(y), and recycle them
  ## to each element of `x` and `y`:
  sx <- .group_sum_int(xo, gnc)
  ux <- (sx/gn)[gi]
  sy <- .group_sum_int(yo, gnc)
  uy <- (sy/gn)[gi]

  ## (x - mean(x)) and (y - mean(y))
  x_ux <- xo - ux
  y_uy <- yo - uy

  ## Slopes!
  x_ux.y_uy <- .group_sum_int(x_ux * y_uy, gnc)
  x_ux2 <- .group_sum_int(x_ux ^ 2, gnc)
  setNames(x_ux.y_uy / x_ux2, grle[['values']])
}

The non-obvious steps involve gn, gnc, and gi. As we saw earlier with group_sum gn corresponds to how many elements there are in each group, and gnc to the index of the last element in each group. Let’s illustrate with some toy values:

(xo <- 2:6)                              # some values

[1] 2 3 4 5 6

(go <- c(3, 3, 5, 5, 5))                 # their groups

[1] 3 3 5 5 5

(gn <- rle(go)[['lengths']])             # the size of the groups

[1] 2 3

(gnc <- cumsum(gn))                      # index of last item in each group

[1] 2 5

Since these are the same quantities used by group_sum, we can use a simpler version .group_sum_int that takes the index of the last element in each group as an input:

(sx <- .group_sum_int(xo, gnc))          # group sum

[1]  5 15

We re-use gnc four times throughout the calculation, which is a big deal because that is the slow step in the computation. With the group sums we can derive the $\bar{x}$ values:

(sx/gn)                                 # mean of each group

[1] 2.5 5.0

But we need to compute $x - \bar{x}$, which means we need to recycle each group’s $\bar{x}$ value for each $x$. This is what gi does:

(gi <- rep(seq_along(gn), gn))

[1] 1 1 2 2 2

cbind(x=xo, ux=(sx/gn)[gi], g=go)  # cbind to show relationship b/w values

     x  ux g
[1,] 2 2.5 3
[2,] 3 2.5 3
[3,] 4 5.0 5
[4,] 5 5.0 5
[5,] 6 5.0 5

For each original $x$ value, we have associated the corresponding $\bar{x}$ value. We compute uy the same way as ux, and once we have those two values the rest of the calculation is straightforward.

While this is quite a bit of work, the results are remarkable:

sys.time(slope.gs <- group_slope(x, y, grp))

   user  system elapsed 
  1.794   0.486   2.312 

Compare to the hand-optimized version of data.table from one of our earlier posts:

sys.time({
  DT <- data.table(x, y, grp)
  setkey(DT, grp)
  DTsum <- DT[, .(ux=mean(x), uy=mean(y)), keyby=grp]
  DT[DTsum, `:=`(x_ux=x - ux, y_uy=y - uy)]
  DT[, `:=`(x_ux.y_uy=x_ux * y_uy, x_ux2=x_ux^2)]
  DTsum <- DT[, .(x_ux.y_uy=sum(x_ux.y_uy), x_ux2=sum(x_ux2)), keyby=grp]
  slope.dt <- DTsum[, .(grp, V1=x_ux.y_uy / x_ux2)]
})

   user  system elapsed 
  2.721   0.412   3.139 

Oh snap, we’re ~30% faster than data.table! And this is the painstakingly optimized version of it that computes on groups directly in C code without the per-group R evaluation overhead. We’re ~3x faster than the straight “out-of-the-box” version DT[, slope(x, y), grp].

A summary of all the timings:

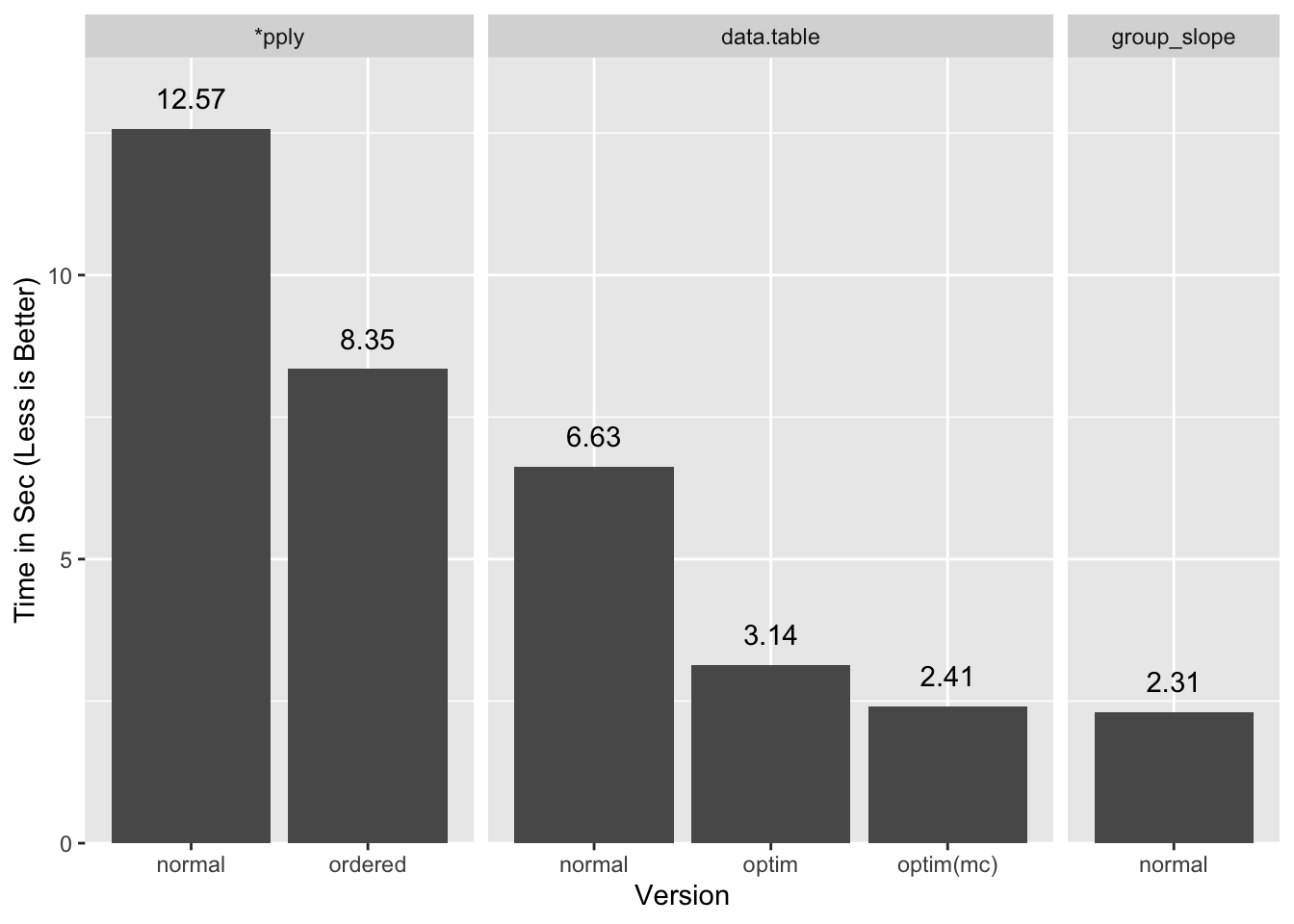
If I let data.table use both my cores it comes close to our timings (optim(mc)), and presumably would do a little better still with more cores, but a tie or a slight win for a multi-thread process over a single thread one is a loss in my books.

More details for the benchmarks are in the appendix.

UPDATE: Michael Chirico points out that it is possible to reformulate the slope equation into a more favorable form, and under that form data.table is faster (although our methods are close). I’ll defer analysis of how generalizable this is to another post, but in the meantime you can see those benchmarks in the appendix.

Controversy

As we bask in the glory of this upset we notice a hubbub around the judges table. A representative of the Commission on Precise Statics, gesticulating, points angrily at us. Oops. It turns out that our blazing fast benchmark hero is cutting some corners:

all.equal(slope.gs, slope.dt$V1, check.attributes=FALSE)

[1] "Mean relative difference: 0.0001161377"

cor(slope.dt$V1, slope.gs, use='complete.obs')

[1] 0.9999882

The answers are almost the same, but not exactly. Our cumsum approach is exhausting the precision available in double precision numerics. We could remedy this by using a rowsums based group_slope, but that would be slower as we would not be able to re-use the group index data.

Oh, so close. We put up a good fight, but CoPS is unforgiving and we are disqualified.

Conclusions

We learned how we can use ordered data to our advantage, and did something quite remarkable in the process: beat data.table at its own game, but for a technicality. Granted, this was for a more complex statistic. We will never be able to beat data.table for simple statistics with built-in gforce counterparts (e.g. sum, median, etc.), but as soon as we step away from those we have a chance, and even for those we are competitive⁷.

In Part 3 of the Hydra Chronicles we will explore why we’re running into precision issues and whether we can redeem ourselves (hint: we can).

Appendix

sessionInfo()

R version 3.6.0 (2019-04-26)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS Mojave 10.14.5

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] data.table_1.12.2

sys.time <- function(exp, reps=11) {
  res <- matrix(0, reps, 5)
  time.call <- quote(system.time({NULL}))
  time.call[[2]][[2]] <- substitute(exp)
  gc()
  for(i in seq_len(reps)) {
    res[i,] <- eval(time.call, parent.frame())
  }
  structure(res, class='proc_time2')
}
print.proc_time2 <- function(x, ...) {
  print(
    structure(
      x[order(x[,3]),][floor(nrow(x)/2),],
      names=c("user.self", "sys.self", "elapsed", "user.child", "sys.child"),
      class='proc_time'
) ) }

o <- order(grp)
go <- grp[o]
xo <- x[o]
sys.time({
  gn <- rle(go)[['lengths']]
  gi <- rep(seq_along(gn), gn)
  gnc <- cumsum(gn)
})

   user  system elapsed
  0.398   0.134   0.535

sys.time(.group_sum_int(xo, gnc))

   user  system elapsed
  0.042   0.008   0.050

sys.time({
  id <- seq_along(grp)
  id.split <- split(id, grp)
  slope.ply <- vapply(id.split, function(id) slope(x[id], y[id]), 0)
})

   user  system elapsed
 12.416   0.142  12.573

all.equal(slope.ply, c(slope.rs), check.attributes=FALSE)

[1] TRUE

sys.time({
  o <- order(grp)
  go <- grp[o]
  id <- seq_along(grp)[o]
  id.split <- split(id, go)
  slope.ply2 <- vapply(id.split, function(id) slope(x[id], y[id]), 0)
})

   user  system elapsed 
  8.233   0.105   8.351 

all.equal(slope.ply2, c(slope.rs), check.attributes=FALSE)

[1] TRUE

setDTthreads(1)
DT <- data.table(grp, x, y)
sys.time(DT[, slope(x, y), grp])

   user  system elapsed 
  6.509   0.066   6.627 

setDTthreads(0)
DT <- data.table(grp, x, y)
sys.time(DT[, slope(x, y), grp])

   user  system elapsed 
  7.979   0.112   6.130 

library(data.table)
setDTthreads(1)
sys.time({
  DT <- data.table(grp, x, y)
  setkey(DT, grp)
  DTsum <- DT[, .(ux=mean(x), uy=mean(y)), keyby=grp]
  DT[DTsum, `:=`(x_ux=x - ux, y_uy=y - uy)]
  DT[, `:=`(x_ux.y_uy=x_ux * y_uy, x_ux2=x_ux^2)]
  DTsum <- DT[, .(x_ux.y_uy=sum(x_ux.y_uy), x_ux2=sum(x_ux2)), keyby=grp]
  res.slope.dt2 <- DTsum[, .(grp, V1=x_ux.y_uy / x_ux2)]
})

   user  system elapsed 
  2.721   0.412   3.139 

setDTthreads(0)
sys.time({
  DT <- data.table(grp, x, y)
  setkey(DT, grp)
  DTsum <- DT[, .(ux=mean(x), uy=mean(y)), keyby=grp]
  DT[DTsum, `:=`(x_ux=x - ux, y_uy=y - uy)]
  DT[, `:=`(x_ux.y_uy=x_ux * y_uy, x_ux2=x_ux^2)]
  DTsum <- DT[, .(x_ux.y_uy=sum(x_ux.y_uy), x_ux2=sum(x_ux2)), keyby=grp]
  res.slope.dt2 <- DTsum[, .(grp, V1=x_ux.y_uy / x_ux2)]
})

   user  system elapsed 
  5.332   0.842   2.412 

sys.time({
  DT <- data.table(x, y, xy=x*y, x2=x^2, grp)
  slope.dt.re <- DT[,
    .(ux=mean(x), uy=mean(y), uxy=mean(xy), ux2=mean(x2)),
    keyby=grp
  ][,
    setNames((uxy - ux*uy)/(ux2 - ux^2), grp)
  ]
})

   user  system elapsed
  1.377   0.126   1.507

quantile(slope.ply2 - slope.dt.re, na.rm=TRUE)

           0%           25%           50%           75%          100% 
-6.211681e-04 -4.996004e-16  0.000000e+00  4.996004e-16  1.651546e-06 

group_slope_re <- function(x, y, grp) {
  o <- order(grp)
  go <- grp[o]
  xo <- x[o]
  yo <- y[o]

  grle <- rle(go)
  gn <- grle[['lengths']]
  gnc <- cumsum(gn)              # Last index in each group

  ux <- .group_sum_int(xo, gnc)/gn
  uy <- .group_sum_int(yo, gnc)/gn
  uxy <- .group_sum_int(xo * yo, gnc)/gn
  ux2 <- .group_sum_int(xo^2, gnc)/gn

  setNames((uxy - ux * uy)/(ux2 - ux^2), grle[['values']])
}
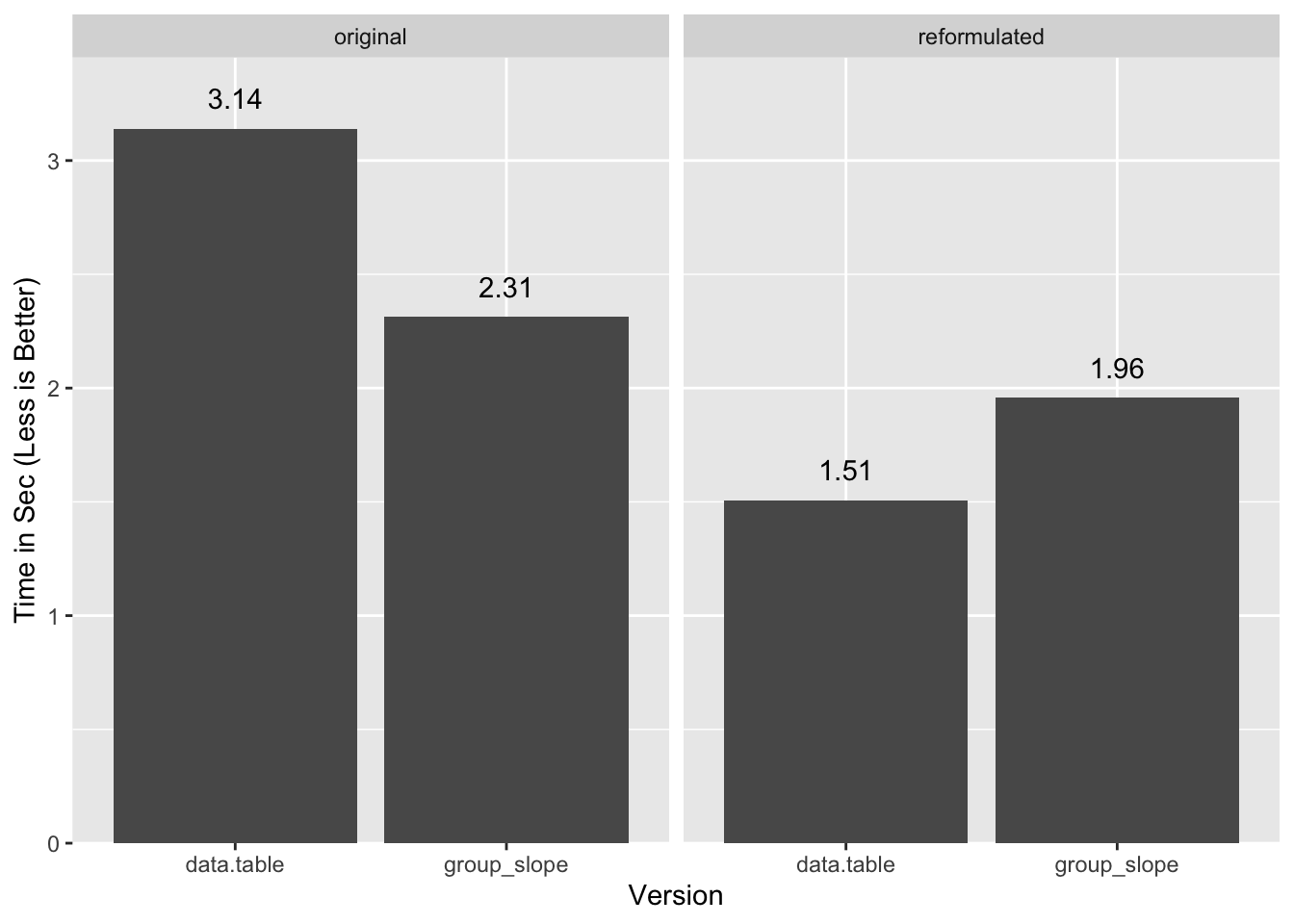
sys.time(slope.gs.re <- group_slope_re(x, y, grp))

   user  system elapsed 
  1.548   0.399   1.957 

group_sum <- function(x, grp) {
  ## Order groups and values
  ord <- order(grp)
  go <- grp[ord]
  xo <- x[ord]

  ## Last values
  grle <- rle(go)
  gnc <- cumsum(grle[['lengths']])
  xc <- cumsum(xo)
  xc.last <- xc[gnc]

  ## Take diffs and return
  gs <- diff(c(0, xc.last))
  setNames(gs, grle[['values']])
}

group_sum2 <- function(x, grp, na.rm=FALSE) {
  if(length(x) != length(grp)) stop("Unequal length args")
  if(!(is.atomic(x) && is.atomic(y))) stop("Non-atomic args")
  if(anyNA(grp)) stop("NA vals not supported in `grp`")

  ord <- order(grp)
  grp.ord <- grp[ord]
  grp.rle <- rle(grp.ord)
  grp.rle.c <- cumsum(grp.rle[['lengths']])
  x.ord <- x[ord]

  # NA and Inf handling. Checking inf makes this 5% slower, but
  # doesn't seem worth adding special handling for cases w/o Infs

  has.na <- anyNA(x)
  if(has.na) {
    na.x <- which(is.na(x.ord))
    x.ord[na.x] <- 0
  } else na.x <- integer()
  inf.x <- which(is.infinite(x.ord))
  any.inf <- length(inf.x) > 0
  if(any.inf) {
    inf.vals <- x.ord[inf.x]
    x.ord[inf.x] <- 0
  }
  x.grp.c <- cumsum(x.ord)[grp.rle.c]
  x.grp.c[-1L] <- x.grp.c[-1L] - x.grp.c[-length(x.grp.c)]

  # Re-inject NAs and Infs as needed

  if(any.inf) {
    inf.grps <- findInterval(inf.x, grp.rle.c, left.open=TRUE) + 1L
    inf.rle <- rle(inf.grps)
    inf.res <- rep(Inf, length(inf.rle[['lengths']]))
    inf.neg <- inf.vals < 0

    # If more than one Inf val in group, need to make sure we don't have
    # Infs of different signs as those add up to NaN
    if(any(inf.long <- (inf.rle[['lengths']] > 1L))) {
      inf.pos.g <- group_sum2(!inf.neg, inf.grps)
      inf.neg.g <- group_sum2(inf.neg, inf.grps)
      inf.res[inf.neg.g > 0] <- -Inf
      inf.res[inf.pos.g & inf.neg.g] <- NaN
    } else {
      inf.res[inf.neg] <- -Inf
    }
    x.grp.c[inf.rle[['values']]] <- inf.res
  }
  if(!na.rm && has.na)
    x.grp.c[findInterval(na.x, grp.rle.c, left.open=TRUE) + 1L] <- NA

  structure(x.grp.c, groups=grp.rle[['values']], n=grp.rle[['lengths']])
}
sys.time(x.grpsum2 <- group_sum2(x, grp))

   user  system elapsed 
  1.147   0.323   1.479 

all.equal(x.grpsum, x.grpsum2)

[1] TRUE