Last year’s RTINI Part I post introduces the RTIN mesh approximation algorithm. In this post we vectorize the algorithm so that it may be efficient in R.
Vectorize The Absolute $#!+ Out Of This

I wish I could tell you that I carefully figured out all the intricacies of the RTIN algorithm before I set off on my initial vectorization attempt, that I didn’t waste hours going cross-eyed at triangles poorly drawn on scraps of paper, and that I didn’t produce algorithms which closer inspection showed to be laughably incorrect. Instead I’ll have to be content with telling you that I did get this to work eventually.
It turns out that that truly understanding an algorithm you’re trying to re-implement is fairly important. Who woulda thunk?
Some Triangles Are More Equal Than Others
The root cause of my early failures at re-implementing @mourner’s
martini is that there are more different types of triangles than is
obvious at first glance. They are all isoceles right angled
triangles, but there are eight possible orientations and each
orientation is only valid at specific locations in the mesh.
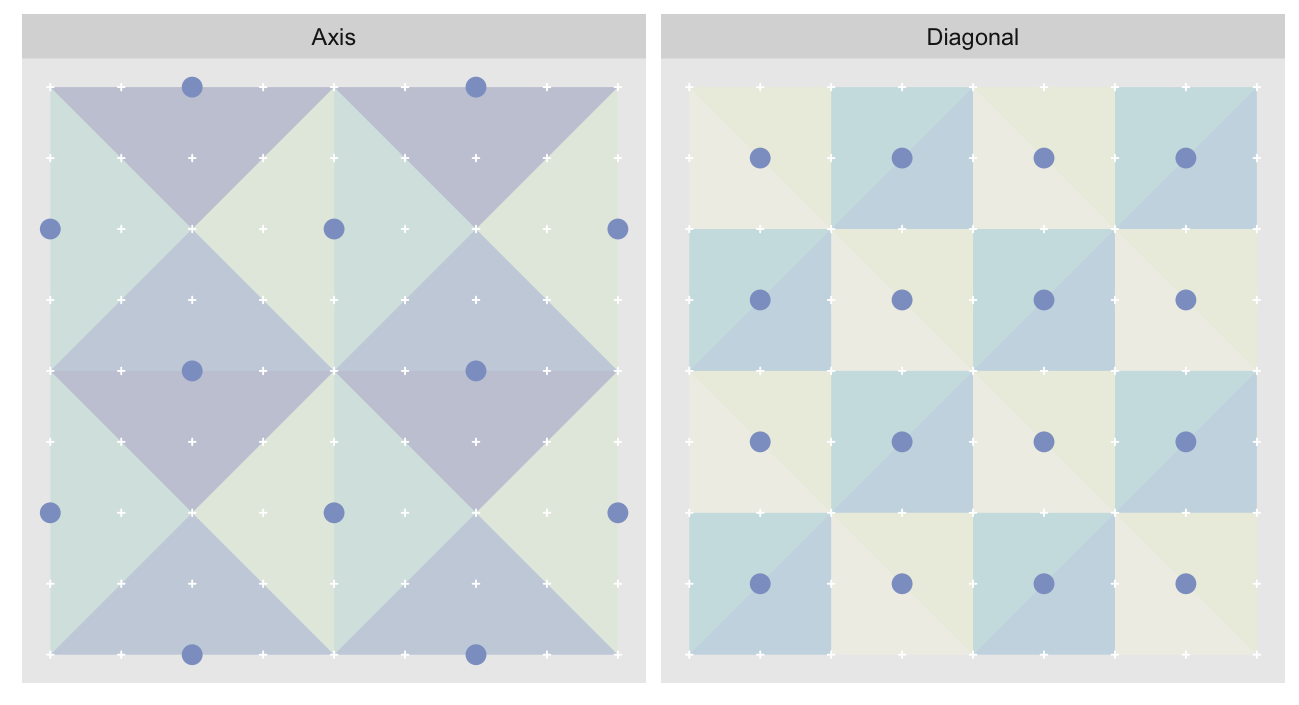
The orientations can be split into two groups of four, with the groups alternating between approximation levels. Here we show the orientations for the 2nd and 3rd most granular levels of a 9 x 9 grid1. The triangles are colored by orientation. Because we’re very imaginative we’ll call the group diagonal hypotenuses “Diagonal”, and the one with vertical/horizontal ones “Axis”:
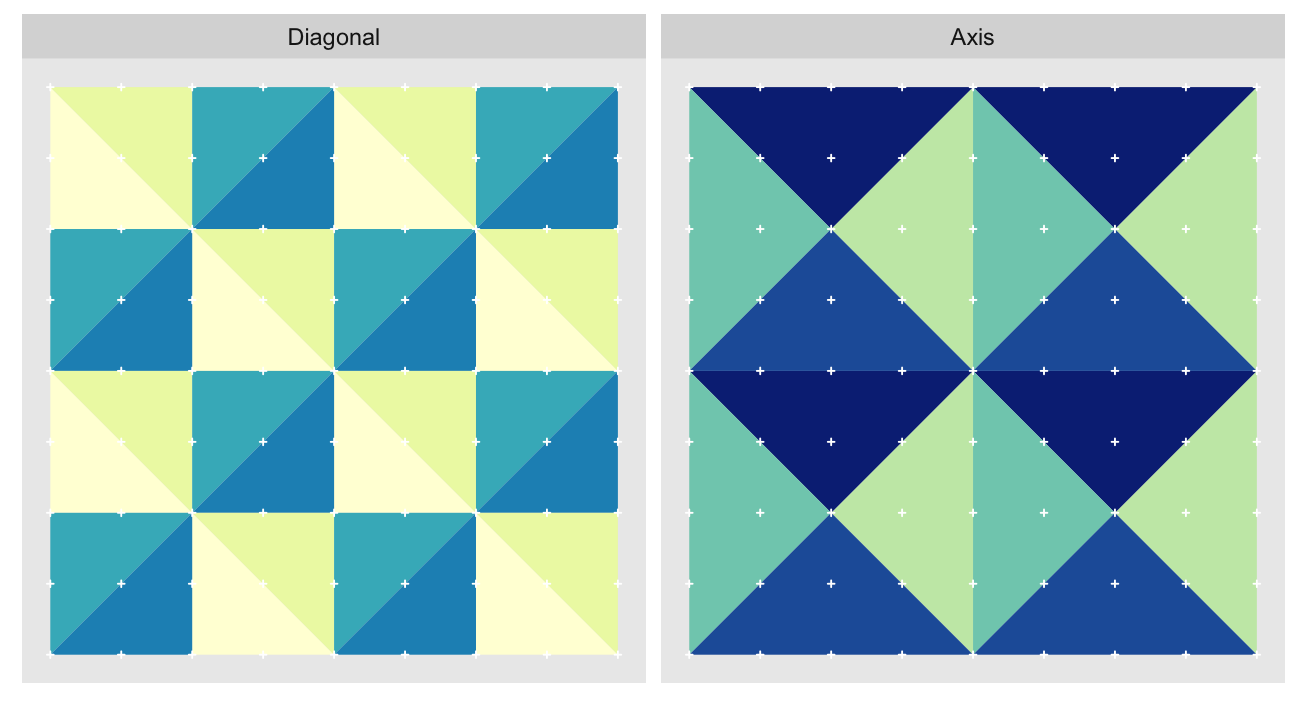
The “Axis” triangulation, the one with vertical and horizontal hypotenuses, has just one tiling pattern. A particular triangle “shape” (a specific color in the plot above) must always be arranged in the same way relative to the other shapes that share the vertex opposite their hypotenuses. Any other arrangement would prevent us from fully tiling the grid without breaking up triangles.
On the other hand the “Diagonal” triangulation, has multiple possible tilings:
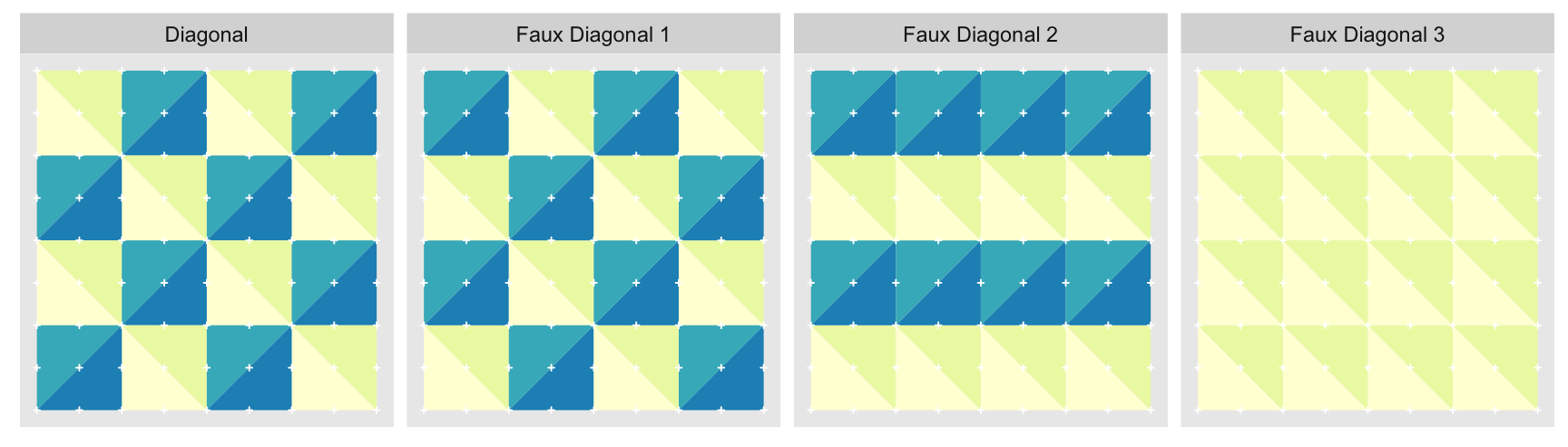
We show just three alternate tilings, although there are . All of them perfectly cover the grid with equal sized triangles. “Faux Diagonal 1” is even a pretty convincing replica. Unfortunately only one of them fits exactly into the next level of coarseness, “Axis” shown previously, seen here in a green outline:
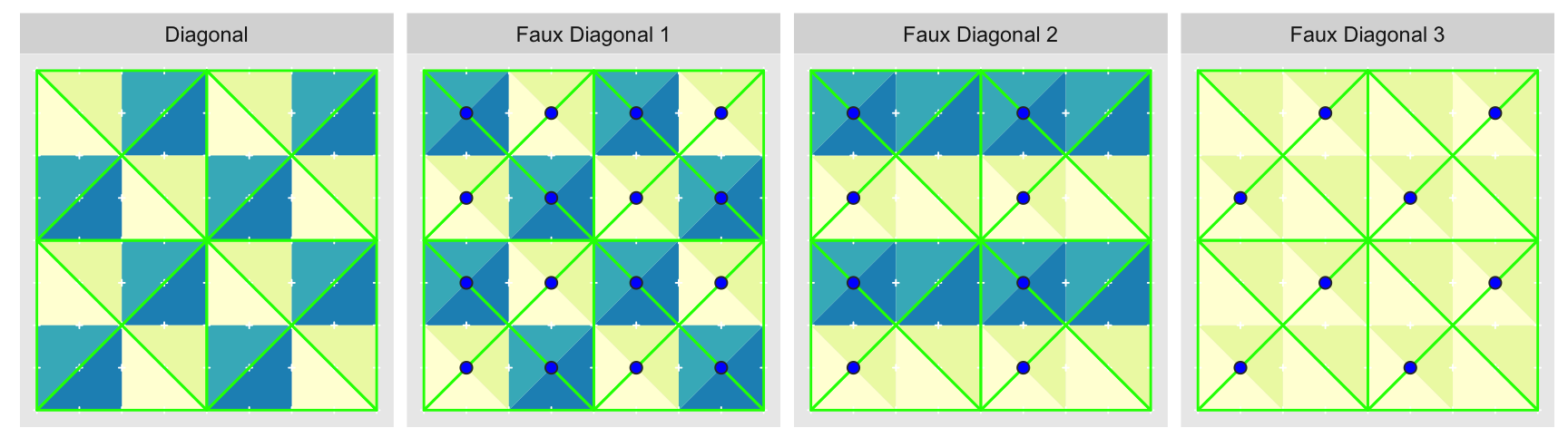
It is only with “Diagonal” that every edge of the parent approximation level completely overlaps with edges of the child. Every other arrangement has at least one parent edge crossing a hypotenuse of a child triangle. These crossings are what the blue circles highlight. Ironically, the best looking fake is the worst offender.
Herein lies the beauty of @mourner’s implementation; by deriving child triangles from splitting the parent ones, we guarantee that the child triangles will conform to the parents. As I learned painfully no such guarantees apply when we compute the coordinates directly.
There are many ways to solve this vectorization problem, but the simplest I could come up with was to treat it as a tiling task. The idea is to define the smallest tessellating patterns that extend to the correct layout. These patterns can then be repeated as needed in internally vectorized manner2. This is what they look like for our 9 x 9 example:

Unfortunately this is insufficient. We must also for each triangle hypotenuse midpoint track their children so that we may carry over their errors. One nice benefit of the tessellating pattern is that if we define the parent-child relationship for the simple tile, we can copy that relationship along with the rest of the tile. In fact, we don’t actually care about the triangles. What we actually want are the hypotenuses (black lines), their midpoints, endpoints, and the corresponding child hypotenuse midpoints. The parent/child relation is shown with the arrows:
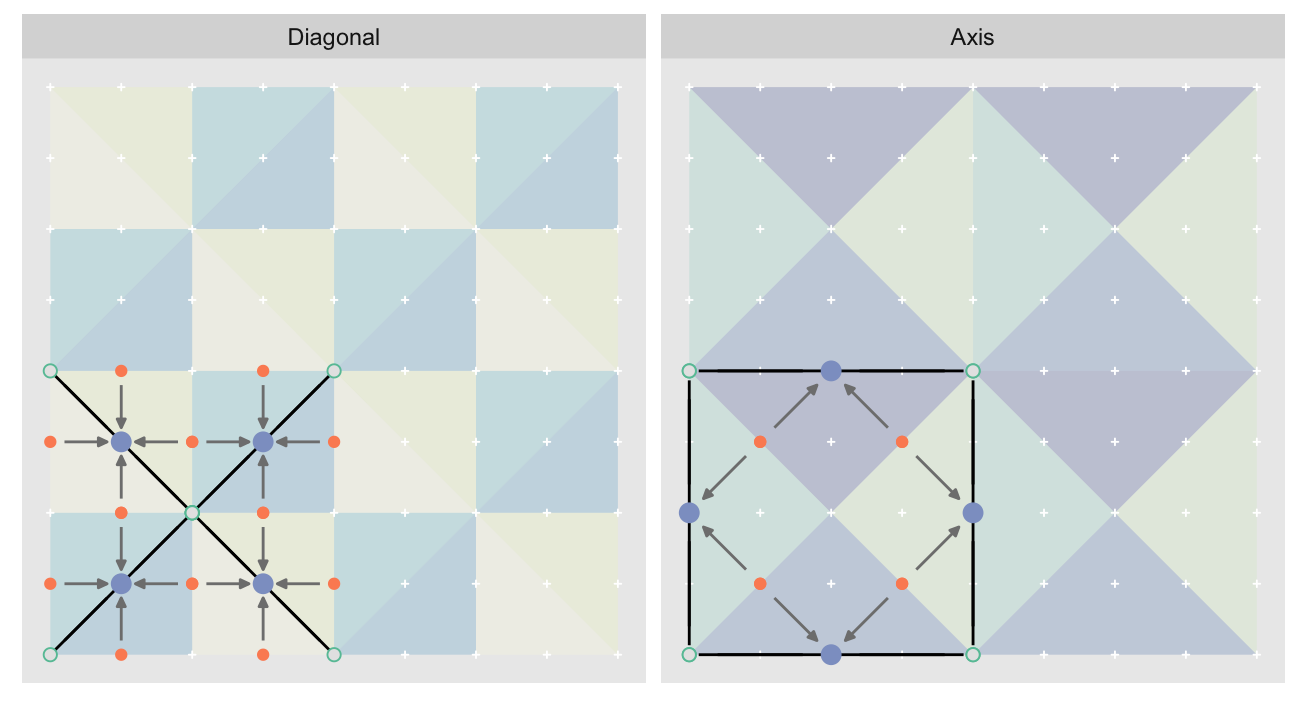
Recall: we are trying to compute the error in approximating the hypotenuse midpoints as the mean of the endpoints, while carrying over error of the child midpoint approximations. Notice how the midpoints of the “Diagonal” layer become the child midpoints in the “Axis” layer.
See RTINI Part I for additional details on the algorithm.
Now Just Tile the Rest of the $#!+ing Map
Great, we have a concept for how we might parallelize the computation of
critical coordinates, but how exactly do we do this in an efficiently vectorized
manner? There are likely many ways, but what we’ll do is use “linearized”
indices into the matrix. These indices treat the matrix as if it were a vector.
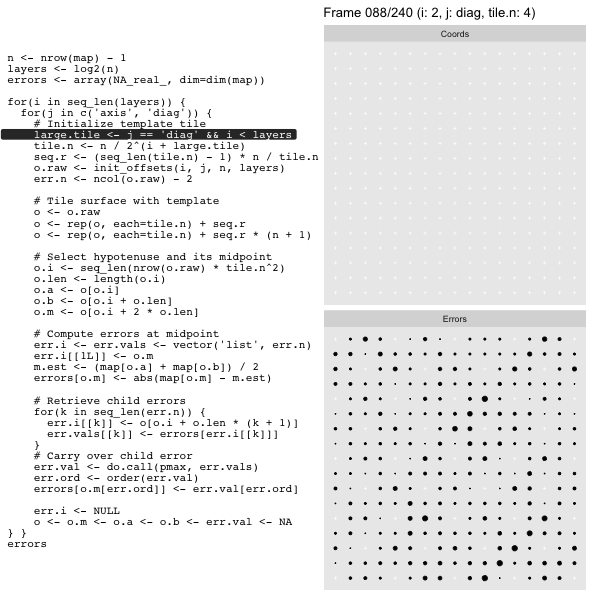
The first step is to generate the template tile, which we will do with
init_offsets, presented here in simplified form3:
init_offsets <- function(i, j, n, layers) {
o <- if(j == 'axis') offset.ax else offset.dg # raw coords
o <- o * 2^(i - 1) # scale
array(o[,1,] + o[,2,] * (n + 1) + 1, dim(o)[-2]) # x/y -> id
}offset.ax and offset.dg are arrays that contain manually computed x/y
coordinates for each of the points in the template tile. init_offsets scales
those to the appropriate size for the layer and collapses them to “linearized”
coordinates4. Here is the “Diagonals”
map with the grid points labeled with their “linearized” coordinates and the key
points of the template tile in the same colors as previously:
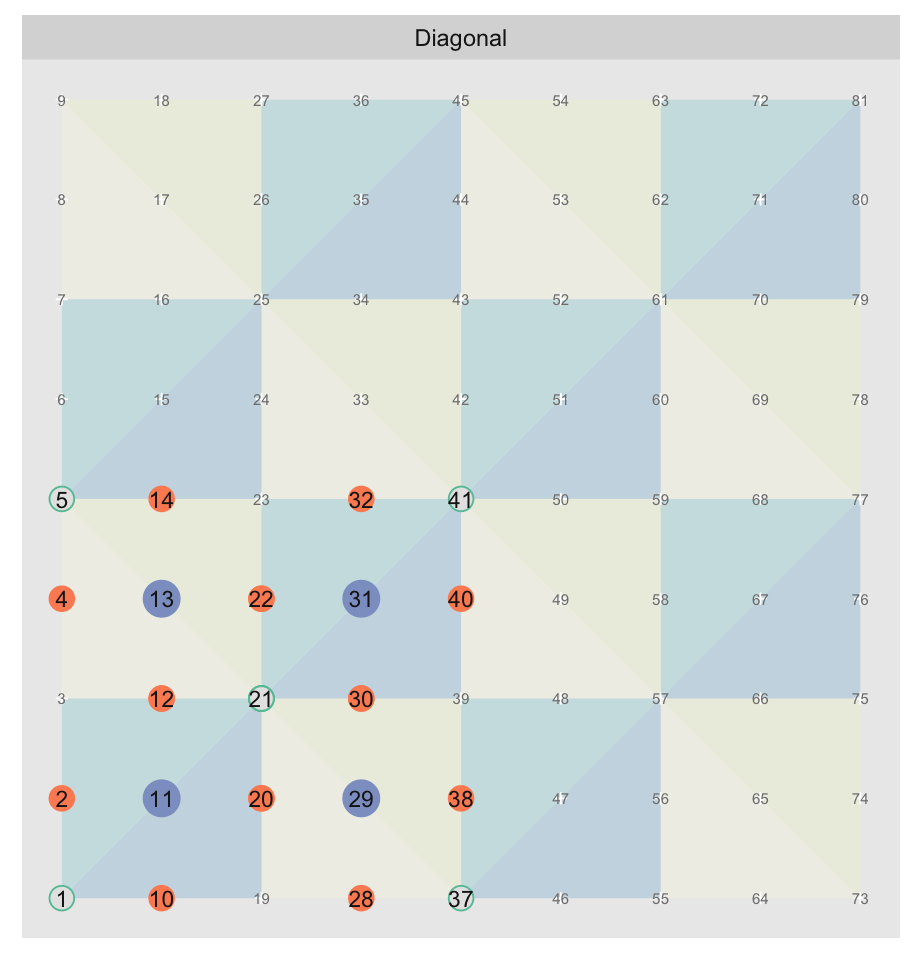
init_offsets produces the coordinates for the template tile:
n <- nrow(map)
init_offsets(i=1, j='diag', n=(n - 1), layers=log2(n - 1)) [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 1 21 11 20 10 2 12
[2,] 5 21 13 22 14 12 4
[3,] 21 37 29 38 30 28 20
[4,] 21 41 31 40 30 22 32
There are repeats as some points are shared across triangles. For example point 21 is a hypotenuse endpoint to all triangles. We can’t just drop the duplicates as the above structure tracks the midpoint by row, and we need the child midpoints and endpoints associated with each of them.
We can shift “linearized” coordinates, by simple arithmetic. For example,
adding one to a coordinate will move it up one row5. Adding
nrow(map) will shift the coordinates by one column. So for example:
init_offsets(i=1, j='diag', n=n - 1, layers=log2(8)) + 4 + 4 * nWould shift the template four rows and four columns to produce:
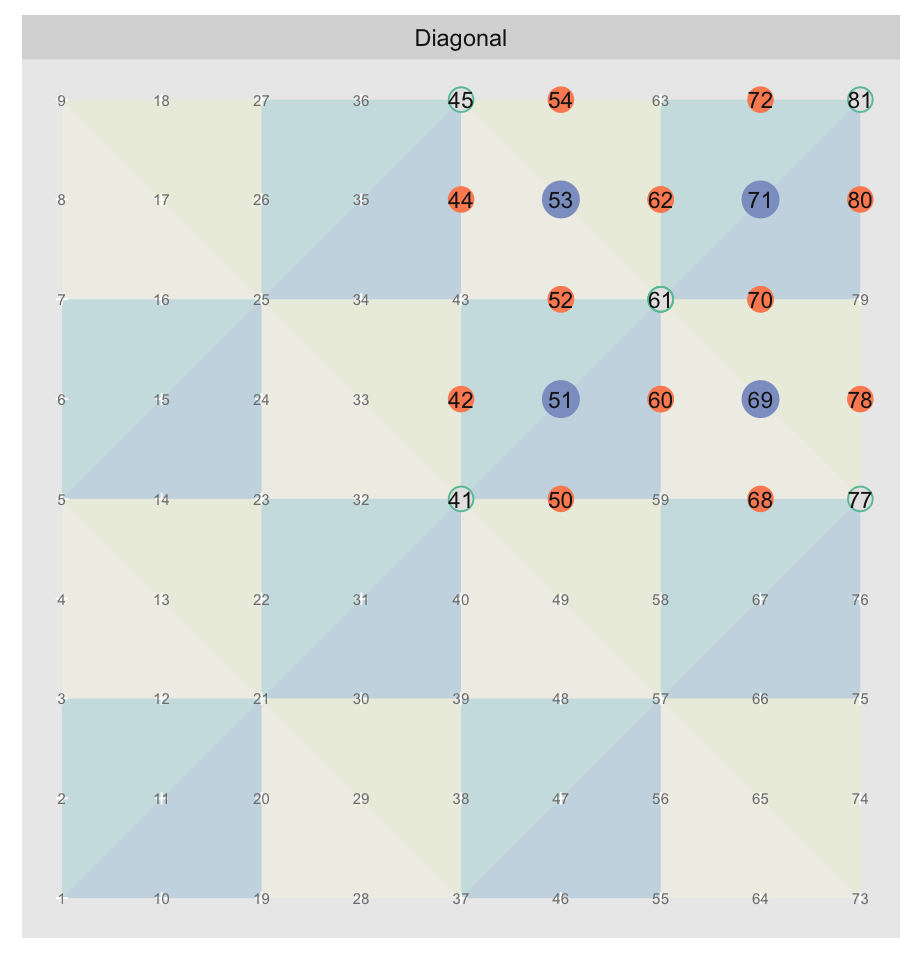
Tiling is then just a matter of copying and shifting the template tile.
Action!
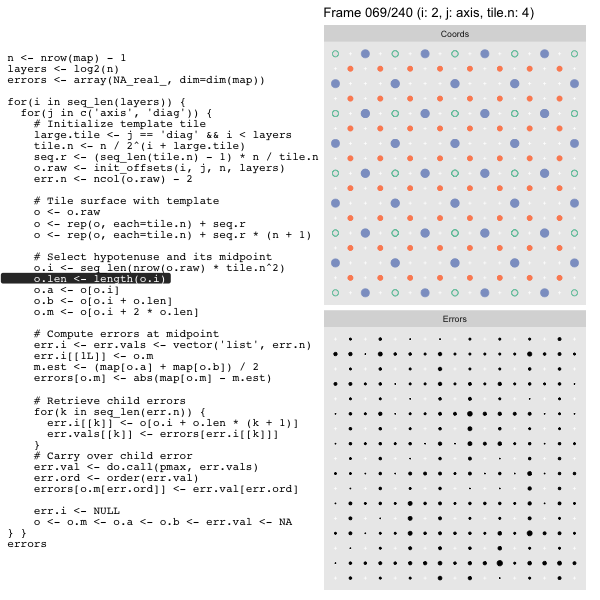
Let’s look at this in action with the next grid size up for effect. As we did in the prior post we’ll track the coordinates in the left panel side (both “Diagonal” and “Axis”, alternating), and the computed mesh approximation errors in the right hand panel:
For each “layer”, we start with a repeatable template sized to the layer. We then fill a column with it, then the rest of the surface, and finally we compute errors. Here is the same thing as a flipbook with code so we can see how it’s actually done. Remember that in these flipbooks the state shown is immediately after the highlighted line is evaluated. We’ll focus on the second set of layers:
FPS: #: / 55
o, as shown in the first frame6 contains the offsets that
represent the template tile. These offsets are generated by init_offsets,
which we reviewed earlier.
Since the tile coordinates are linearized we can shift them by repeating the template while adding different offsets to each repeat:
seq.r <- (seq_len(tile.n) - 1) * n / tile.n
o <- rep(o, each=tile.n) + seq.rWe first repeat the template tile four times (tile.n), and then shift them by
seq.r:
seq.r[1] 0 4 8 12Due to how we repeat o each value of seq.r will be recycled for every value
of o. The result is to copy the template tile to fill the column. Similarly
we can fill the rest of the surface by repeating and shifting the column:
o <- rep(o, each=tile.n) + seq.r * (n + 1)The points are arranged by type in the original offset list so we can easily subset for a particular type of point from the repeated tile set:
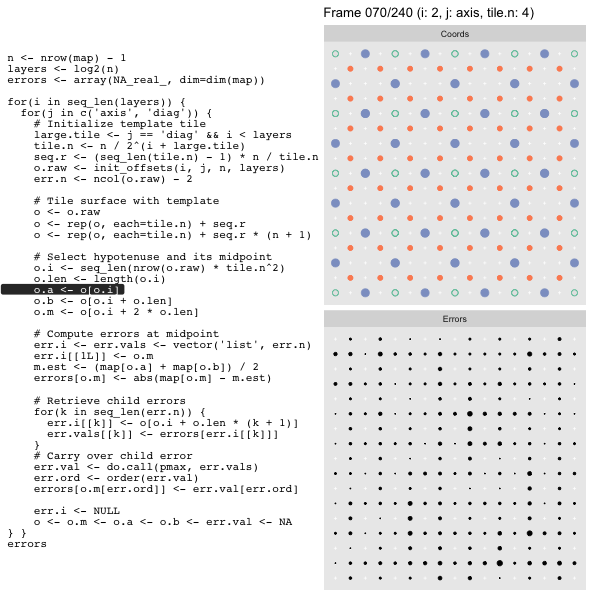
o.m <- o[o.i + 2 * o.len] # midpoint coordinate
o.b <- o[o.i + o.len] # 1st hypotenuse endpoint coordinate
o.a <- o[o.i] # 2nd hypotenuse endpoint coordinateThis is how the visualization knows to color the points as the point type is never explicitly stated in the code. Additionally, the relative positions of parents and children are also preserved.
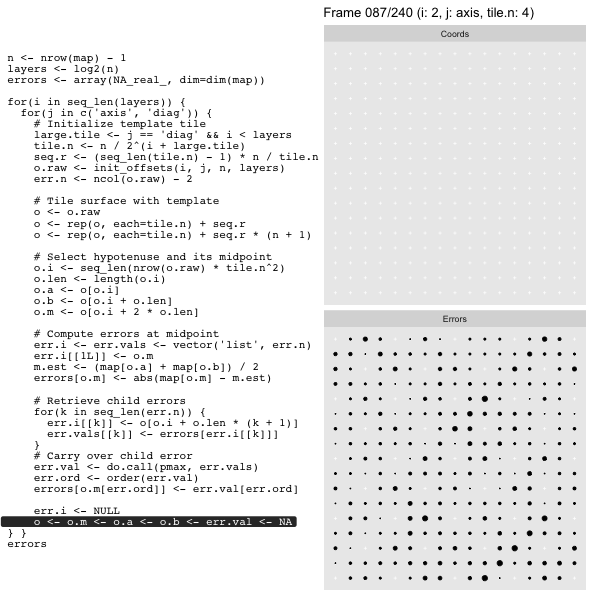
After calculating the errors we must record the maximum of the error and child errors. This includes the following seemingly funny business:
err.val <- do.call(pmax, err.vals)
err.ord <- order(err.val) # <<< Order
errors[o.m[err.ord]] <- err.val[err.ord]This is necessary because for “Axis” tiling the same midpoints may be updated by two different tiles as is the case here when we fill a column:
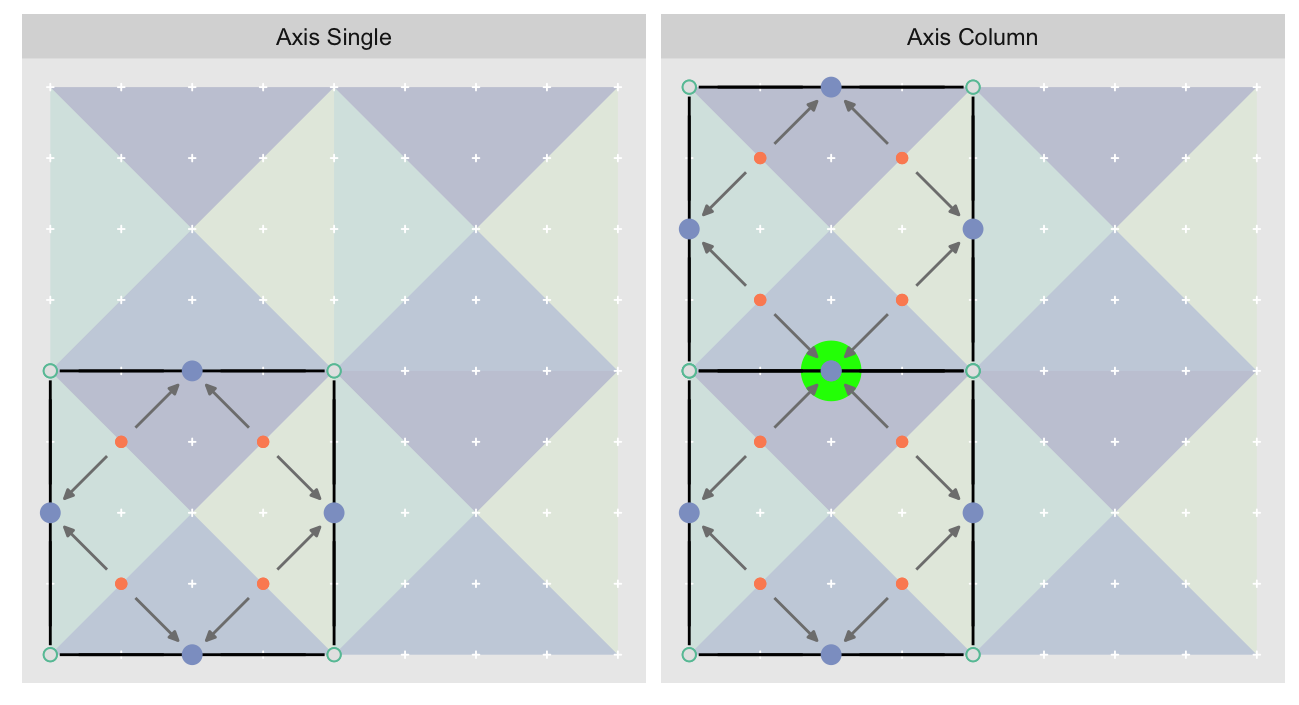
The midpoint highlighted in green is at the overlap of two tiles, so
we are carrying over errors from children in different tiles. If we did not
order err.val prior to final insertion into the error matrix we risk a lesser
error from one tile overwriting a larger error from another. This issue
afflicts all the non-peripheral midpoints in the “Axis” tile
arrangement7.
The full code of this implementation is available in the appendix.
Loopy Vectorization?
Hold on a sec, weren’t we going to vectorize the $#!+ out of this? What about all those for loops? They are nested three levels deep! A veritable viper’s nest of looping control structures. Did we just turn ourselves around and end up with more loops than we started with? Strictly speaking we did, but what matters is how many R-level calls there are, not how many R-level loops. Particularly once we start getting to large map sizes, the bulk of the computations are being done in statically compiled code.
Our vectorized algorithm got through the 17 x 17 map in 240 R-level
steps8. The original one requires 40,962 for the same map! The
vectorized algorithm R-level call count will grow with where n is
the number of rows/cols in the map. The original transliteration will grow with
. There are a similar number of calculations overall, but as
you can see in the animation the vectorized version “batches” many of them into
single R-level calls to minimize the R interpreter overhead. So yes, despite
the for loops our code is very vectorized, and it shows up in the timings:
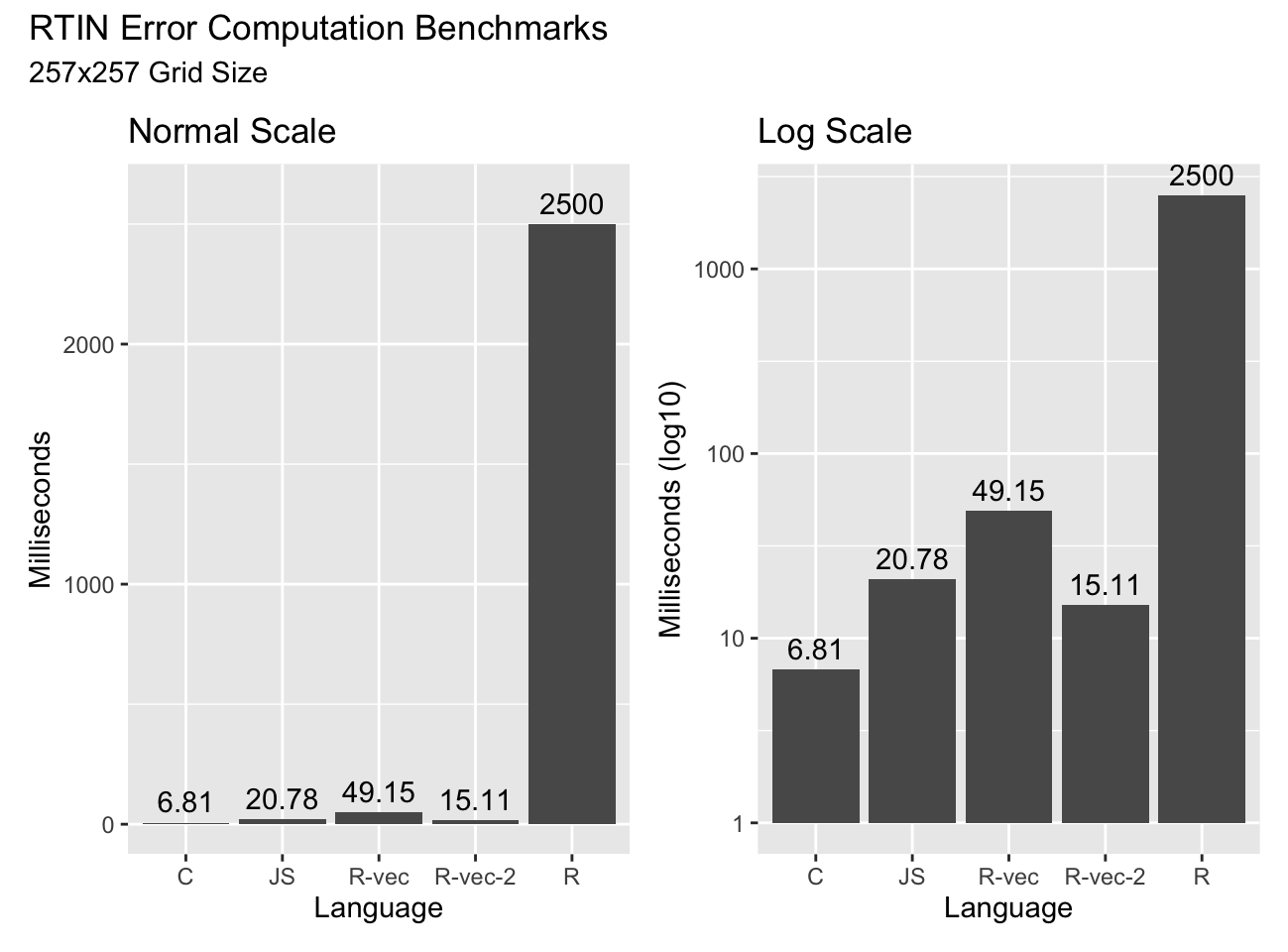
The code as shown (“R-vec”) is about twice as slow as JavaScript, but fifty times faster than the R transliteration of the RTIN algorithm! With some additional optimizations I won’t bore you with (“R-vec-2”) we get to beat out JavaScript. And something remarkable happens as we increase grid sizes:
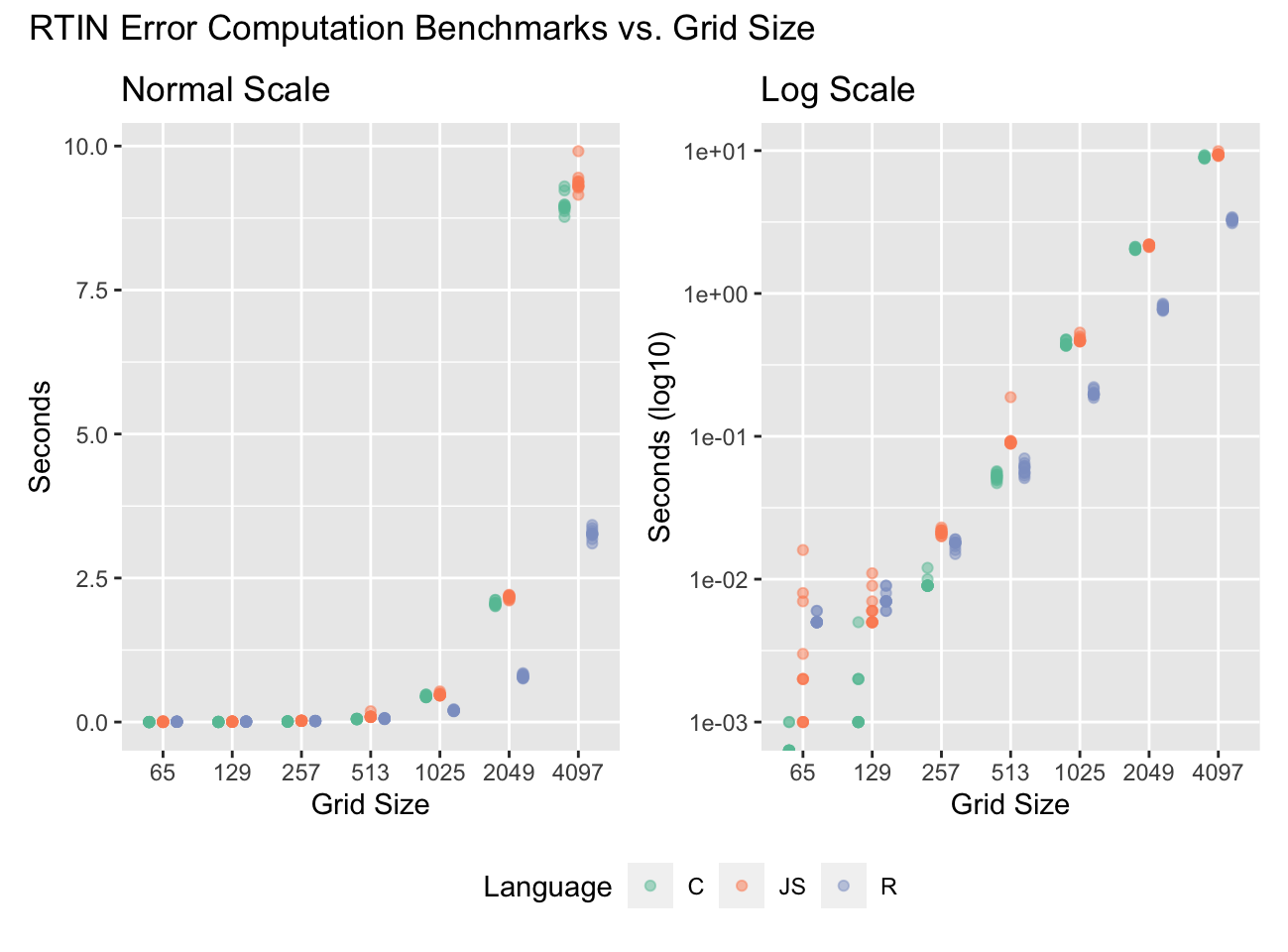
The optimized R implementation (“R-vec-2” from the previous chart) beats both the C and JS implementations by a factor of 2-3x. At the lower sizes the overhead of the R calls holds us back, but as the overall computations increase by , the number of R calls only increase by . As the term grows the vectorized algorithm benefits from requiring fewer steps to compute the midpoints.
It is also remarkable that JS does as well as C, perhaps with some
more timing volatility due to the overhead of invoking V8 via R
and possibly JIT compilation9.
Before we move on, a quick recap of some vectorization concepts we applied here:
- Identify repeating / parallelizable patterns.
- Structure the data so that the repeating patterns can be processed by internally vectorized10 functions.
- Allow R-level loops so long as the number of their iterations is small relative to those carried out in internally vectorized code.
To achieve 2. we resorted to carefully structured seed data, and repeated it either explicitly or implicitly with vector recycling. We did this both for the actual data, as well as for the indices we used to subset the data for use in the vectorized operations.
Too Square
One advantage of directly computing the hypotenuse midpoint coordinates is that we are not limited to square elevation maps. With a little extra work we can make the vectorized R implementation support any rectangular map with an odd number of points in both width and height. The “R-vec-2” implementation does exactly that. This allows us to render the 550 x 505 River Derwent DEM by dropping just one row:
The closest dimensions available to the original algorithm are 257 x 257 or 513 x 513, so this is a pretty good feature. A limitation is that the full range of approximation is only available for the grids the original algorithm supports, but there are many useful cases where this doesn’t matter. The best example is stitching together tiles into a larger map that does not conform to . The most approximate view will be to resolve each tile to two triangles, but there should be no need to go more approximate than that. In exchange you get a larger map with more flexible dimensions that has no inconsistencies at the boundaries, such as this one:

Limits of Vectorization
So far we have completely avoided discussion of the second part of the RTIN algorithm: extraction of approximate meshes subject to an error tolerance. Here an R implementation does worse, but still impressively if we consider that the JavaScript version is JIT compiled into machine code:
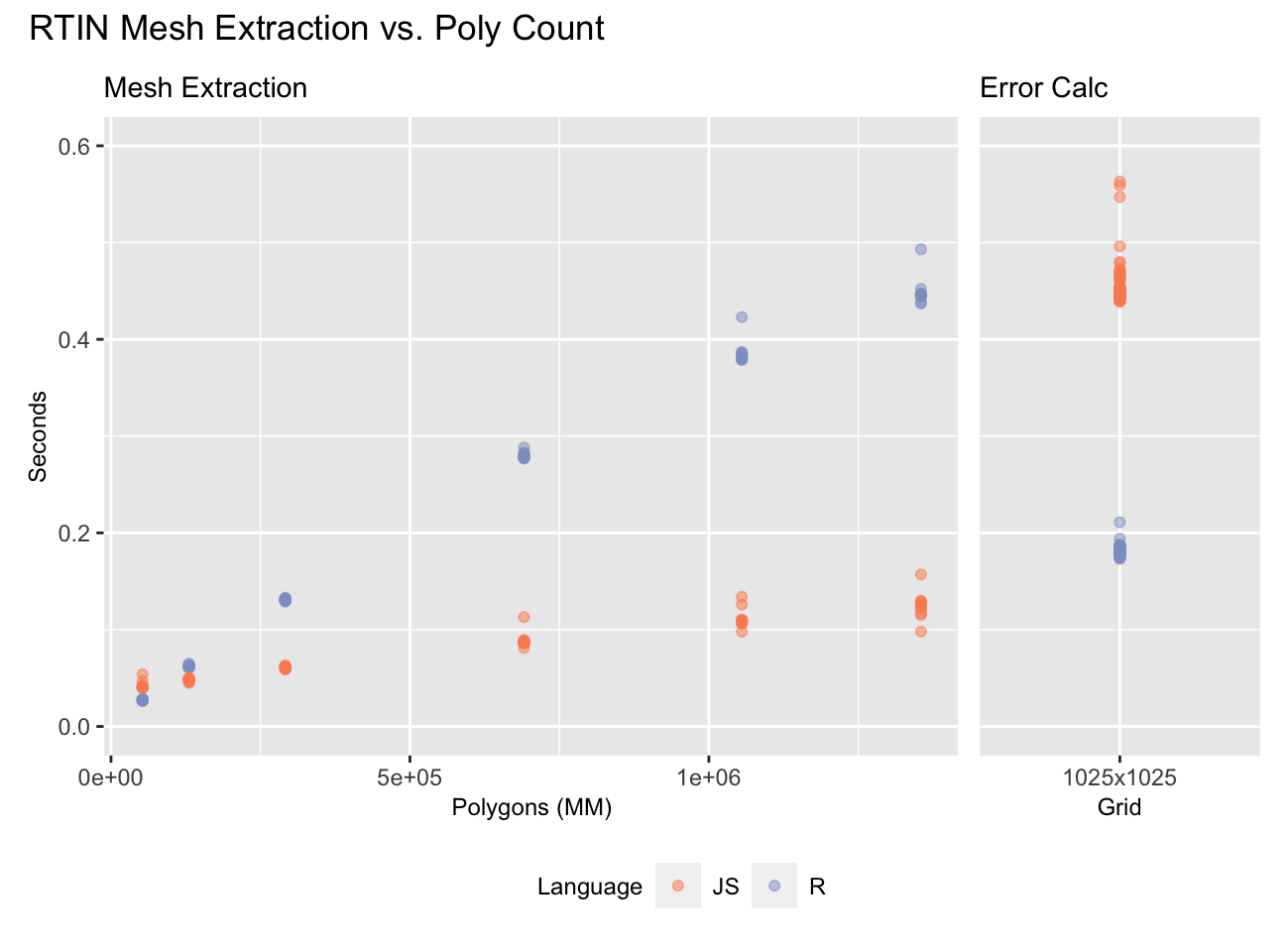
On the 1025 x 1025 grid we tested JS is about as much faster at extracting the meshes (left) as R is at computing the errors (right). How much this matters is a function of how many polygons you extract. The full mesh contains about 2MM polygons, but it looks good with few as ~200K polygons:



These are all the River Derwent DEM repeated kaleidoscope style to fill 1025 x 1025 maps.
R is able to beat out JavaScript and even C in the error computation because the RTIN algorithm is quite “inefficient”11. Watch it in action again and notice how many steps it takes to compute the location of the first point to compute the error at on a 5 x 5 grid. Compare to how many steps we need with the vectorized algorithm to compute every error on a much larger grid, including child error carry over. I would expect that if we implemented the R version of the algorithm in JavaScript the latter would be faster, assuming the JIT compilation can be as effective as it is with the RTIN algorithm.
Even when algorithms can be fully internally vectorized12 R is at a disadvantage, usually because vectors need to be re-arranged which requires generating indices and making copies of the vectors. Notwithstanding, for such algorithms it is often possible to get close enough to statically compiled performance that the R implementation is satisfactory.
Conclusions

Despite R being saddled with interpreter overhead, it is often possible to write it in such a way that performance is comparable to statically compiled code. Sometimes it is easy, sometimes it isn’t. Was it worth it in this case? Well, I learned a bit from the process so in the end it was worth it to me. And as a result of this we now have a base-R-only mesh reduction algorithm that works on a much broader set of meshes than the original RTIN.
Questions, comments, or just want to share this post? Post about it on Twitter. Follow @brodiegaslam for updates and/or new post notifications.
Appendix
Acknowledgments
The following are post-specific acknowledgments. This website owes many additional thanks to generous people and organizations that have made it possible.
- Vladimir Agafonkin for writing great posts and for introducing me to the RTIN algorithm.
- Tyler Morgan Wall for
rayrenderwith which I made many of the illustrations in this post. Special thanks for the endless stream of new features, including bump-mapping for simulating rippling water, preview mode to make it easy to set-up scenes, and many more. - Michael Sumner for inspiring me to vectorize the absolute shit out of this.
- Thomas Lin Pedersen for
patchworkwith which I assembled the combined plots in this post, and forambientwith which I created the water surface maps (based on a Tyler Morgan Wall gist). - Hadley Wickham and the
ggplot2authors forggplot2with which I made many the plots in this post. - Jeroen Ooms for R interface to
V8which I used to benchmark the JavaScriptmartiniimplementation. - Simon Urbanek for the PNG package which I used while post-processing many of the images in this post.
- The FFmpeg team for FFmpeg with which I stitched the frames off the videos in this post.
- Oleg Sklyar, Dirk Eddelbuettel, Romain François, etal. for
inlinefor easy integration of C code into ad-hoc R functions. - Cynthia Brewer for color brewer palettes, one of which I used in some plots, and axismaps for the web tool for picking them.
Follies in Optimization
If you’ve read any of my previous blog posts you probably realize by now that I have a bit of a thing <cough>unhealthy obsession</cough> for making my R code run fast. I wouldn’t put what’s coming next into the “premature optimization is the root of all evil” category, but rational people will justifiable question why anyone would spend as much time as I have trying to make something that doesn’t need to be any faster, faster.
A potential improvement over the initial vectorized implementation is to directly compute the midpoint locations. As we can see here they are arranged in patterns that we should be able to compute without having to resort to tiling:
For each layer all the children will be at fixed offsets from the midpoints. The hypotenuses orientations vary within a layer, so we can’t use fixed offsets for them. However, if we split the midpoints into two groups (A and B below) we can use fixed offsets within each group. For “Diagonal” the groups are bottom-left to top-right (A) and top-left to bottom-right (B), and for “Axis” vertical (A) and horizontal (B):

All is not perfect though: “Axis” is again a problem as the peripheral midpoints end up generating out-of-bounds children, shown as hollow points / dashed arrows above. I won’t get into the details, but handling the out-of-bounds children requires separate treatment for the left/top/right/bottom periphery as well as the inner midpoints. We need to handle far more corner cases than with the template approach which makes the code much uglier.
Grid Flexibility Limitations
The vectorized RTIN algorithm will work on any rectangular height map with an
odd number of rows and columns, but it will work better with some than others.
For example it works with volcano, but the maximum approximation level is not
even throughout the surface:
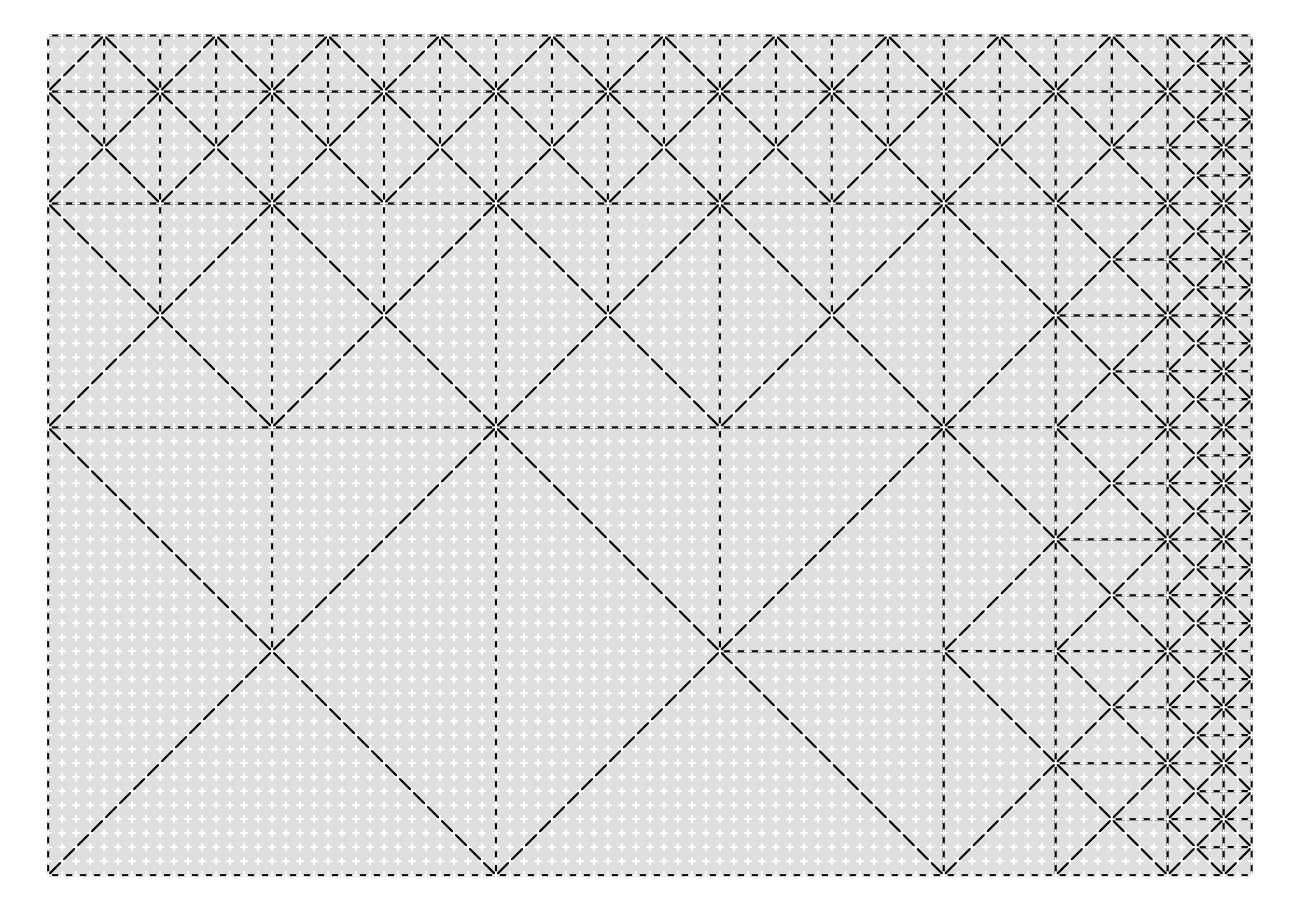
As we get closer to the top and right edges the largest triangle size we can use and still conform with the rest of the mesh becomes smaller and smaller. If instead of 87 x 61 volcano was 97 x 65 then we would get a much better most-approximated mesh:
The best grids for the R implementation will be , and those that are will be pretty good too. So long as we are satisfied with maximum approximation to be , we can assemble any tiling of tiles that size into rectangles and we’ll be assured to have self consistent extracted meshes.
Code Appendix
This is the implementation shown in the flipbook. We recommend you the optimized version from the RTINI package if you are intending on using it.
# Offsets are: parenta, parentb, h midpoint, children with variable number of
# children supported
offset.dg <- aperm(
array(
c(
0L,0L, 2L,2L, 1L,1L, 1L,2L, 0L,1L, 1L,0L, 2L,1L,
4L,0L, 2L,2L, 3L,1L, 3L,2L, 4L,1L, 2L,1L, 3L,0L,
2L,2L, 0L,4L, 1L,3L, 1L,4L, 2L,3L, 0L,3L, 1L,2L,
2L,2L, 4L,4L, 3L,3L, 3L,4L, 2L,3L, 3L,2L, 4L,3L
),
dim=c(2L, 7L, 4L)
),
c(3L, 1L, 2L)
)
# Smallest size that allows us to define the children with integer
# values.
offset.ax <- aperm(
array(
c(
0L,0L, 4L,0L, 2L,0L, 3L,1L, 1L,1L,
4L,0L, 4L,4L, 4L,2L, 3L,3L, 3L,1L,
4L,4L, 0L,4L, 2L,4L, 1L,3L, 3L,3L,
0L,4L, 0L,0L, 0L,2L, 1L,1L, 1L,3L
),
dim=c(2L, 5L, 4L)
),
c(3L, 1L, 2L)
)
init_offsets <- function(i, j, n, layers) {
axis <- j == 'axis'
o.raw <- if(axis) offset.ax else offset.dg
if(!axis && i == layers)
o.raw <- o.raw[1L,,,drop=F]
if(axis && i == 1L)
o.raw <- o.raw[,,1:3,drop=F]
o.raw <- (o.raw * 2^i) %/% (if(axis) 4L else 2L)
array(o.raw[,1L,] + o.raw[,2L,] * (n + 1L) + 1L, dim(o.raw)[-2L])
}
compute_error3b <- function(map) {
n <- nrow(map) - 1
layers <- log2(n)
errors <- array(NA_real_, dim=dim(map))
for(i in seq_len(layers)) {
for(j in c('axis', 'diag')) {
## Initialize template tile
large.tile <- j == 'diag' && i < layers
tile.n <- n / 2^(i + large.tile)
o <- init_offsets(i, j, n, layers)
o.dim <- dim(o)
## Tile rest of surface using template
seq.r <- (seq_len(tile.n) - 1) * n / tile.n
o <- rep(o, each=tile.n) + seq.r
o <- rep(o, each=tile.n) + seq.r * (n + 1)
## Identify hypotenuse and its midpoint
o.i <- seq_len(o.dim[1] * tile.n^2)
o.len <- length(o.i)
o.m <- o[o.i + 2 * o.len]
o.b <- o[o.i + o.len]
o.a <- o[o.i]
## Compute estimate and error at midpoint
m.est <- (map[o.a] + map[o.b]) / 2
errors[o.m] <- abs(map[o.m] - m.est)
## Retrieve child errors
err.n <- o.dim[2] - 2
err.i <- err.vals <- vector('list', err.n)
for(k in seq_len(err.n)) {
err.i[[k]] <- o[o.i + o.len * (k + 1)]
err.vals[[k]] <- errors[err.i[[k]]]
}
## Carry over child errors
err.val <- do.call(pmax, err.vals)
err.ord <- order(err.val)
errors[o.m[err.ord]] <- err.val[err.ord]
err.i <- NULL
o <- o.m <- o.a <- o.b <- err.val <- NA
} }
errors
}Session Info
R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] inline_0.3.17 patchwork_1.1.0 ambient_1.0.0 rayrender_0.19.0
[5] vetr_0.2.12
loaded via a namespace (and not attached):
[1] Rcpp_1.0.5 compiler_4.0.3 pillar_1.4.7 later_1.1.0.1
[5] tools_4.0.3 jsonlite_1.7.1 lifecycle_0.2.0 tibble_3.0.4
[9] gtable_0.3.0 pkgconfig_2.0.3 rlang_0.4.9 rstudioapi_0.13
[13] yaml_2.2.1 blogdown_0.21 xfun_0.19 dplyr_1.0.2
[17] stringr_1.4.0 roxygen2_7.1.1 xml2_1.3.2 knitr_1.30
[21] generics_0.1.0 vctrs_0.3.5 tidyselect_1.1.0 grid_4.0.3
[25] glue_1.4.2 R6_2.5.0 processx_3.4.5 bookdown_0.21
[29] ggplot2_3.3.2 purrr_0.3.4 magrittr_2.0.1 servr_0.20
[33] scales_1.1.1 ps_1.4.0 promises_1.1.1 ellipsis_0.3.1
[37] colorspace_2.0-0 httpuv_1.5.4 stringi_1.5.3 munsell_0.5.0
[41] crayon_1.3.4Some tiling issues become apparent at this size that are less obvious at smaller sizes.↩
Internally vectorized operations loop through elements of a vector with statically compiled code instead of explicit R loops such as
for,lapply.↩The actual implementation needs to handle several special cases, such as the largest size “Diagonal” that only contains one hypotenuse instead of the typical four, and the smallest size “Axis” that does not have any children. The unused variable
layersis used to identify the corner cases in the full version.↩@mourner’s implementation used this approach, and since it saves space and may be faster computationally I adopted it. To preserve my sanity I transpose the coordinates in the actual implementation so that the matrix representation aligns with the plotted one (i.e. x corresponds to columns, y to rows, albeit with y values in the wrong direction). In other words,
x <- (id - 1) %/% nrow(map), andy <- (id - 1) %% nrow(map)↩But watch out for row shifts that cause column shifts, or column shifts that take you out of bounds.↩
First frame in the flipbook, but step 65 in the overall animation.↩
In the “Diagonal” tiles the midpoints are on the inside of the tile so there is no overlap issue.↩
We’re under-counting as the calls used in the vectorized version tend to be more complex, and we also have
init_offsetsthat hides some calls.↩I made some small changes to the JavaScript implementation for ease if interchange with R via the V8 package. Most significant is that we no longer use 32 bit floats. JavaScript is actually a little faster than C when using 32 bit floats, which makes sense since the C implementation is using doubles. Additionally, for mesh extraction we pre-allocate a vector of maximal possible size rather than using a Geometry object as I did not want to have to chase down what that was and how to use it. You can inspect the JS versions of the code used in this post yourself if you’re curious.↩
Internally vectorized operations loop through elements of a vector with statically compiled code instead of explicit R loops such as
for,lapply.↩I use quotes here because the inefficiency isn’t necessarily bad. The RTIN algorithm handles many corner cases gracefully by virtue of how it computes the triangle hypotenuse midpoints, and it is efficient enough to be useful.↩
Internally vectorized operations loop through elements of a vector with statically compiled code instead of explicit R loops such as
for,lapply.↩